在线性代数中，线性变换是一个核心概念，线性变换的一种特殊情况是可逆线性变换，它在许多领域，包括物理学、工程学、计算机科学等都有广泛应用，本文将详细介绍可逆线性变化的规范表述，包括其定义、性质、应用以及存在的相关问题。

可逆线性变换的定义

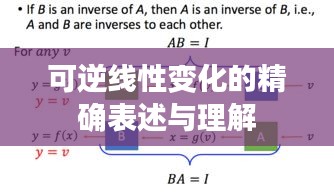
在线性代数中，线性变换是一种保持空间结构不变的变换，对于给定的线性空间V，如果存在一个线性变换T，使得对于V中的任意两个向量α和β，都有T(α+β)=T(α)+T(β)和T(kα)=kT(α)（k为标量），则称T为V上的线性变换，当线性变换存在逆变换时，称之为可逆线性变换，换句话说，如果存在一个线性变换T^-1，使得T^-1T=TT^-1=I（I为单位变换），则线性变换T是可逆的。

可逆线性变换的性质

1、非奇异性：可逆线性变换的矩阵表示是非奇异的，即其行列式不为零。

2、唯一性：给定线性空间中的两个向量，经过可逆线性变换后，它们的关系是唯一的。

3、矩阵求逆：可逆线性变换的矩阵可以通过矩阵求逆得到其逆变换的矩阵。

4、保距性：可逆线性变换保持向量间的距离不变。

可逆线性变换的应用

可逆线性变换在各个领域都有广泛的应用，在物理学中，它用于描述物理系统的动态行为；在工程学中，它用于解决电路分析、控制系统等问题；在计算机科学中，它用于图像处理、数据压缩等，可逆线性变换还在矩阵对角化、解线性方程组等方面发挥重要作用。

可逆线性变化的规范表述

对于可逆线性变化，我们需要规范其表述方式以确保准确性和清晰性，我们需要明确其定义和性质，在描述可逆线性变化时，我们应使用准确的数学语言和符号，我们可以使用矩阵来表示线性变换，并使用矩阵乘法来表示变换的运算，我们还需要注意描述可逆线性变化的上下文和背景，以便读者能够更好地理解其应用。

存在的问题

在实际应用中，有时会出现关于可逆线性变换的误解和混淆，这可能是由于对概念的理解不清或者表述不准确导致的，为了避免这些问题，我们需要更加规范地表述可逆线性变化，包括其定义、性质、应用等，我们还需要提供更多的实例和练习题，以帮助读者更好地掌握可逆线性变换的应用。

可逆线性变换是线性代数中的一个重要概念，具有广泛的应用，为了更好地理解和应用可逆线性变换，我们需要规范其表述方式，本文详细介绍了可逆线性变化的定义、性质、应用以及存在的问题，希望能对读者有所帮助。